Seismic Data Compression#
In this page we will be showing compression performance of MDIO.
For demonstration purposes, we will use one of the Volve dataset stacks. The dataset is licensed by Equinor and Volve License Partners under Equinor Open Data Licence. License document and further information can be found here.
We are using the 3D seismic stack dataset named ST10010ZC11_PZ_PSDM_KIRCH_FAR_D.MIG_FIN.POST_STACK.3D.JS-017536.segy.
However, for convenience, we renamed it to volve.segy.
Warning
The examples below need the following extra dependencies:
Matplotlib for plotting.
Scikit-image for calculating metrics.
Please install them before executing using pip or conda.
Note
Even though we demonstrate with Volve here, this notebook can be run with any seismic dataset.
If you are new to MDIO we recommend you first look at our quick start guide
from mdio import segy_to_mdio, MDIOReader
Ingestion#
We will ingest three files:
Lossless mode
Lossy mode (with default tolerance)
Lossy mode (with more compression, more relaxed tolerance)
Lossless (Default)#
segy_to_mdio(
"volve.segy",
"volve.mdio",
(189, 193),
# lossless=True,
# compression_tolerance=0.01,
)
print("Done.")
Done.
Lossy Default#
Equivalent to tolerance = 0.01.
segy_to_mdio(
"volve.segy",
"volve_lossy.mdio",
(189, 193),
lossless=False,
# compression_tolerance=0.01,
)
print("Done.")
Done.
Lossy+ (A Lot of Compression)#
Here we set tolerance = 1. This means all our errors will be comfortably under 1.0.
segy_to_mdio(
"volve.segy",
"volve_lossy_plus.mdio",
(189, 193),
lossless=False,
compression_tolerance=1,
)
print("Done.")
Done.
Observe Sizes#
Since MDIO uses a hierarchical directory structure, we provide a convenience function to get size of it using directory recursion and getting size.
import os
def get_dir_size(path: str) -> int:
"""Get size of a directory recursively."""
total = 0
with os.scandir(path) as it:
for entry in it:
if entry.is_file():
total += entry.stat().st_size
elif entry.is_dir():
total += get_dir_size(entry.path)
return total
def get_size(path: str) -> int:
"""Get size of a folder or a file."""
if os.path.isfile(path):
return os.path.getsize(path)
elif os.path.isdir(path):
return get_dir_size(path)
print(f"SEG-Y:\t{get_size('volve.segy') / 1024 / 1024:.2f} MB")
print(f"MDIO:\t{get_size('volve.mdio') / 1024 / 1024:.2f} MB")
print(f"Lossy:\t{get_size('volve_lossy.mdio') / 1024 / 1024:.2f} MB")
print(f"Lossy+:\t{get_size('volve_lossy_plus.mdio') / 1024 / 1024:.2f} MB")
SEG-Y: 1305.02 MB
MDIO: 998.80 MB
Lossy: 263.57 MB
Lossy+: 52.75 MB
Open Files, and Get Raw Statistics#
lossless = MDIOReader("volve.mdio")
lossy = MDIOReader("volve_lossy.mdio")
lossy_plus = MDIOReader("volve_lossy_plus.mdio")
stats = lossless.stats
std = stats["std"]
min_ = stats["min"]
max_ = stats["max"]
Plot Images with Differences#
Let’s define some plotting functions for convenience.
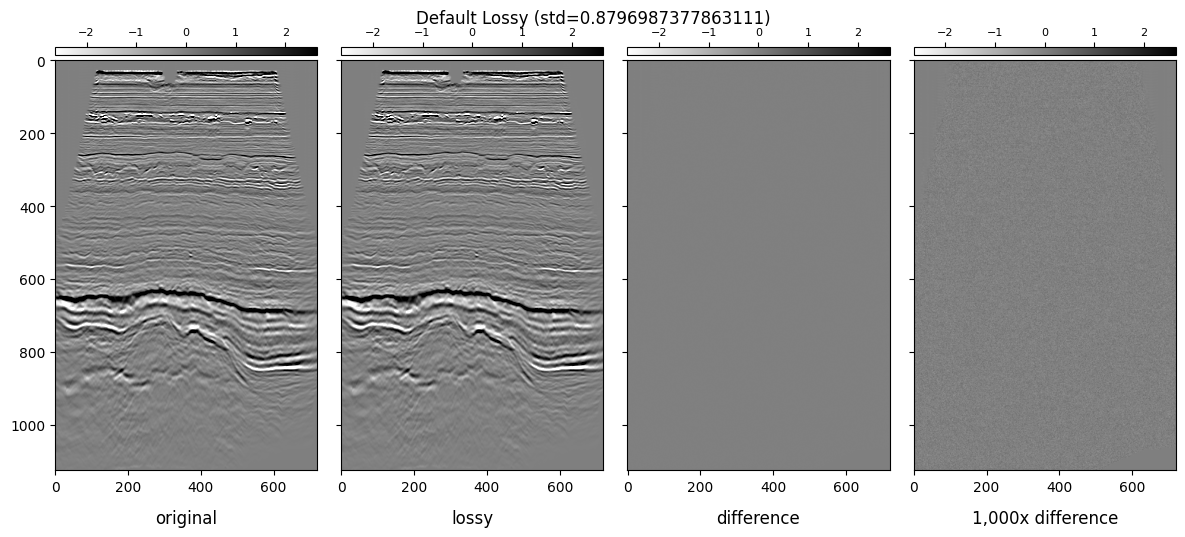
Here, we will make two plots showing data for lossy and lossy+ versions.
We will be showing the following subplots for each dataset:
Lossless Inline
Lossy Inline
Difference
1,000x Gained Difference
We will be using ± 3 * standard_deviation of the colorbar ranges.
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
vmin = -3 * std
vmax = 3 * std
imshow_kw = dict(vmin=vmin, vmax=vmax, cmap="gray_r", interpolation="bilinear")
def attach_colorbar(image, axis):
divider = make_axes_locatable(axis)
cax = divider.append_axes("top", size="2%", pad=0.05)
plt.colorbar(image, cax=cax, orientation="horizontal")
cax.xaxis.set_ticks_position("top")
cax.tick_params(labelsize=8)
def plot_image_and_cbar(data, axis, title):
image = axis.imshow(data.T, **imshow_kw)
attach_colorbar(image, axis)
axis.set_title(title, y=-0.15)
def plot_inlines_with_diff(orig, compressed, title):
fig, ax = plt.subplots(1, 4, sharey="all", sharex="all", figsize=(12, 5))
diff = orig[200] - compressed[200]
plot_image_and_cbar(orig[200], ax[0], "original")
plot_image_and_cbar(compressed[200], ax[1], "lossy")
plot_image_and_cbar(diff, ax[2], "difference")
plot_image_and_cbar(diff * 1_000, ax[3], "1,000x difference")
plt.suptitle(f"{title} ({std=})")
fig.tight_layout()
plt.show()
plot_inlines_with_diff(lossless, lossy, "Default Lossy")
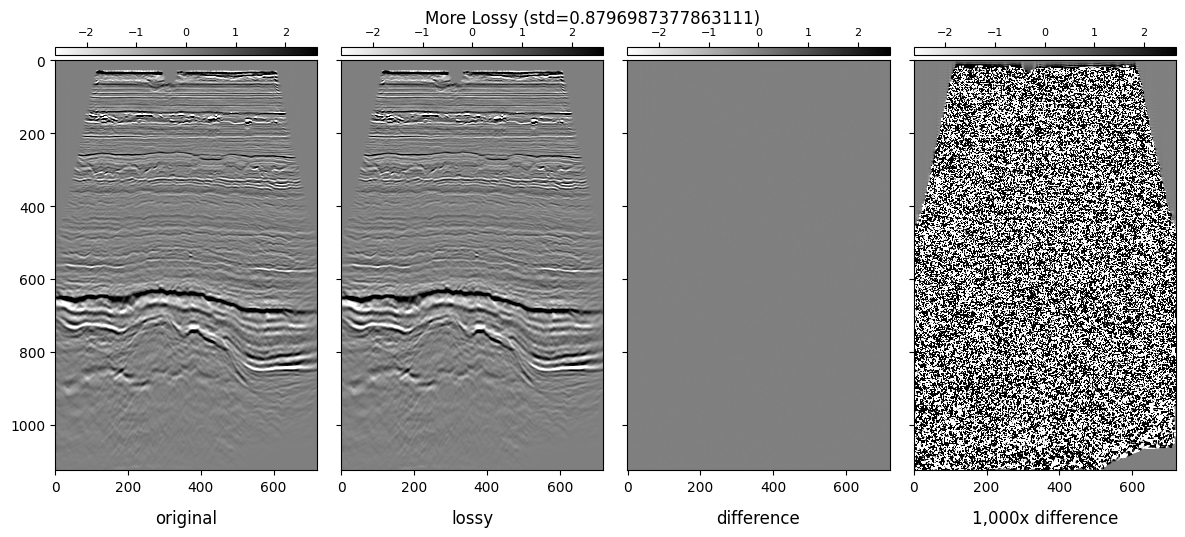
plot_inlines_with_diff(lossless, lossy_plus, "More Lossy")
Calculate Metrics#
For image quality, there are some metrics used by the broader image compression community.
In this example we will be using the following four metrics as comparison.
PSNR: Peak signal-to-noise ratio for an image. (higher is better)
SSIM: Mean structural similarity index between two images. (higher is better, maximum value is 1.0)
MSE: Compute the mean-squared error between two images. (lower is better)
NRMSE: Normalized root mean-squared error between two images. (lower is better)
For PSNR or SSIM, we use the global dataset range (max - min) as the normalization method.
In image compression community, a PSNR value above 60 dB (decibels) is considered acceptable.
We calculate these metrics on the same inline we show above.
import skimage
def get_metrics(image_true, image_test):
"""Get four metrics"""
psnr = skimage.metrics.peak_signal_noise_ratio(
image_true[200], image_test[200], data_range=max_ - min_
)
ssim = skimage.metrics.structural_similarity(
image_true[200], image_test[200], data_range=max_ - min_
)
mse = skimage.metrics.mean_squared_error(image_true[200], image_test[200])
nrmse = skimage.metrics.normalized_root_mse(image_true[200], image_test[200])
return psnr, ssim, mse, nrmse
print("Lossy", get_metrics(lossless, lossy))
print("Lossy+", get_metrics(lossless, lossy_plus))
Lossy (106.69280984265322, 0.9999999784224242, 9.176027503792131e-08, 0.000330489434736117)
Lossy+ (66.27609586061718, 0.999721336954417, 0.0010100110026414078, 0.0346731484815586)